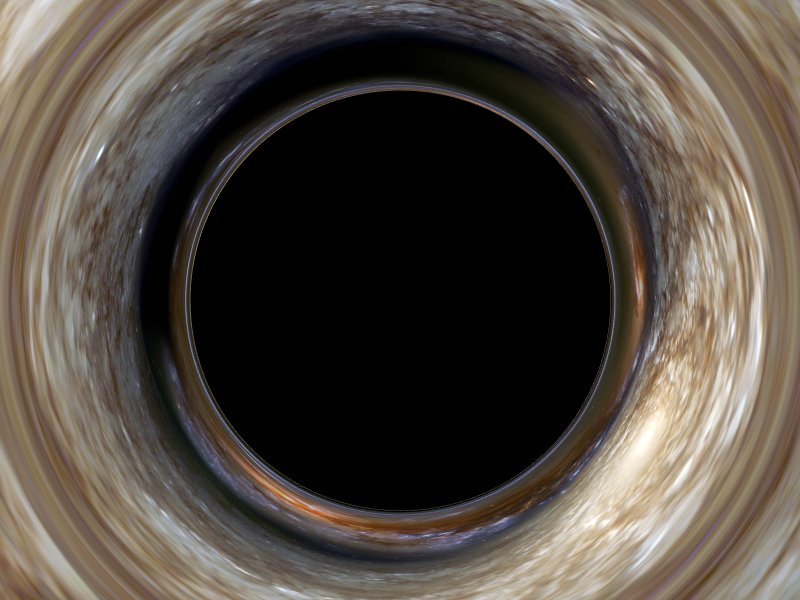
Computer-generated image of a black-hole as seen from a great distance (r=1000M, or 500 times the radius of the event horizon). From this distance, the hole itself is not very conspicuous: the best hope we would have of detecting it from Earth is by observing the brightness changes of a star passing behind it and through the region of optical distortion, which at great distances will appear much larger that the hole itself (scaling in angular size as 1/sqrt(r) rather than 1/r).
Most black holes that astronomers have identified so far have been detected because they are in the process of consuming matter, which emits X-rays due to frictional effects as it spirals into the hole. This simulated one is quiescent and there are predicted to be many such holes in the Galaxy, of roughly 3-10 solar masses, formed by supernovae explosions.

This image was taken from r=100M. The outermost circular anomaly is known as the first 'Einstein ring' and corresponds to the image of a point directly behind the hole. This point would normally be obscured from view, but light passing at this distance from the hole bends through an angle that allows it to reach the observer. Inside this ring, the light at any point actually comes from the opposite side of the hole's apparent position, as the angular deflection increases.
If this were a stellar-mass black hole, humans would not be able to survive at this distance (even in a free fall orbit) because the gravitational tidal gradient is roughly 20 gees per metre. However this effect decreases as the cube of r, so it would be hardly noticable at the distance of the r=1000M picture.
The black hole in this image looks much closer than it really is. The field of view in these images is 90 degrees across and this was taken from r=10M, so the hole appears to have a radius of more than double that of the event horizon (2M). This is because not all of the black area corresponds to rays "blocked" by the hole, just rays that could not reach the observer from infinity, so objects nearer the hole could appear here.
The bending of light is so extreme that much of the light in the inner bands of this image actually comes from behind you. Two more Einstein rings can be seen as a 'double ring' on the edge of the black region. The outer one corresponds to light from directly behind the observer that has done a U-turn about the hole. The inner one (visible only as an arc at the top left) is light from behind the hole, which has orbited 360 degrees before escaping.
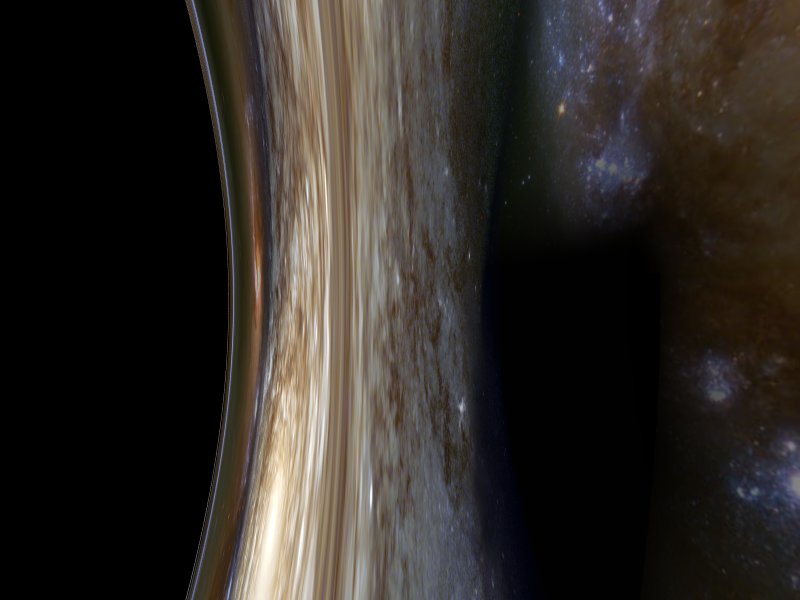
Looking sideways from r=4M.

At r=3M, the hole covers exactly half of the sky: this image is taken looking sideways at an apparently flat "horizon". In fact this is just the same optical effect as in the last picture, but to a greater extent. Below this radius light emitted from infinity will always be spiralling inwards so there will be no light from 'underneath' the observer.
This is also the distance at which there is a circular orbit for photons around the hole, so if we were to shine a torch at the centre of this image, it would do a complete orbit and appear as a light shining from directly behind us.

At r=2.5M, the black hole covers more than half the visible sky, but we are still not within the event horizon.

The whole exterior sky can now by seen in one view by looking directly away from the hole from r=2.2M (everywhere else is black). The Einstein rings are still visible within this view, so in fact it covers the whole sky more than once. Theoretically there are infinitely many Einstein rings, corresponding to light doing greater numbers of half-turns about the hole before escaping to infinity, so there will be infinitely-many distorted images of the sky right near at the edge of this disc. In practice only the first few will ever be visible.

This image is from r=2.05M and shows how the rear view shrinks for observers closer to the event horizon. Note that all these images are calculated for observers who are stationary relative to the outside world (their spatial Schwarzschild coordinates are constant). In reality if you were ever unfortunate enough to be this close to a black hole, you would probably be falling inwards at a significant fraction of the speed of light, so special relativistic effects would make the view rather different. In particular, the view of the outside world would not look this small, because the Lorentz tranformation acts on the sky sphere to reduce the apparent size of objects in front of you and to increase the size of things behind.

![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=2.05M_back.jpg&size=100) r=2.05M_back.jpg
r=2.05M_back.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=2.2M_back.jpg&size=100) r=2.2M_back.jpg
r=2.2M_back.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=2.5M_90deg.jpg&size=100) r=2.5M_90deg.jpg
r=2.5M_90deg.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=3M_90deg.jpg&size=100) r=3M_90deg.jpg
r=3M_90deg.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=4M_90deg.jpg&size=100) r=4M_90deg.jpg
r=4M_90deg.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=10M.jpg&size=100) r=10M.jpg
r=10M.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=10M_23deg.jpg&size=100) r=10M_23deg.jpg
r=10M_23deg.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=100M.jpg&size=100) r=100M.jpg
r=100M.jpg![[jpg]](/hidden/thumb.php?file=misc/blackhole/r=1000M.jpg&size=100) r=1000M.jpg
r=1000M.jpg